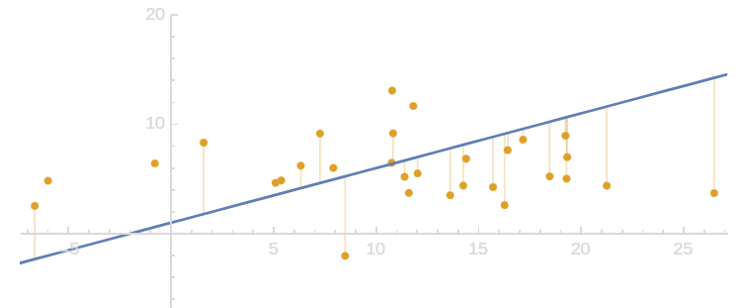
회귀분석 내생성과 이분산의 도식적 이해
회귀식 Regression Equation 기초
$\quad \quad y_i = X_i \beta + \epsilon_i \quad : \quad \epsilon \sim (0, \Omega)$
Homoskedasticity : 오차항 등분산 : $\quad \Omega = \sigma^2 I$
$\quad \quad \hat\beta_{OLS} = (X’X)^{-1}X’y$
Heteroskedasticity : 오차항 이분산 : $\quad \Omega \ne \sigma^2 I$
$\quad \quad \hat\beta_{GLS} = (X’\Omega^{-1}X)^{-1}X’\Omega^{-1}y$
회귀식 추정 및 검정의 핵심 점검사항 2개
1) 오차의 이분산/자기상관 » 효율성 문제 : 보완 및 타협 ???
-
$\beta$ 일치추정은 가능
-
단, $\hat \beta$ 추론(검정)에는 견고한 분산추정량 사용
2) 내생성(endogeneity) : $X$ 와 $\epsilon$ 상관 » 핵심 사항 !!!
- $\beta$ 일치추정 하려면 도구변수 필요
비편향 일치 추정 위해 $X$ 와 $\epsilon$ 의 확률적 관계가 중요
$X$ 가 확률변수 아니면 문제가 매우 쉬워짐
- 자연과학에서 실험으로 통제되는 경우임
그러나 사회과학에서는 실험 어려움
-
$X$ 는 확률변수이며, 자료는 일회적 실현치
-
오차변수 $\epsilon$ 과의 확률적 관계에 따라 방법론 달라짐
$X$ 와 $\epsilon$ 의 확률적 관계 유형
1) 독립적 : 가장 이상적 : OLS 충분
2) 외생적 : $E[\,\epsilon \mid X\,] = 0 \quad \Rightarrow \quad \hat\beta_{OLS}$ 는 비편향(불편)추정
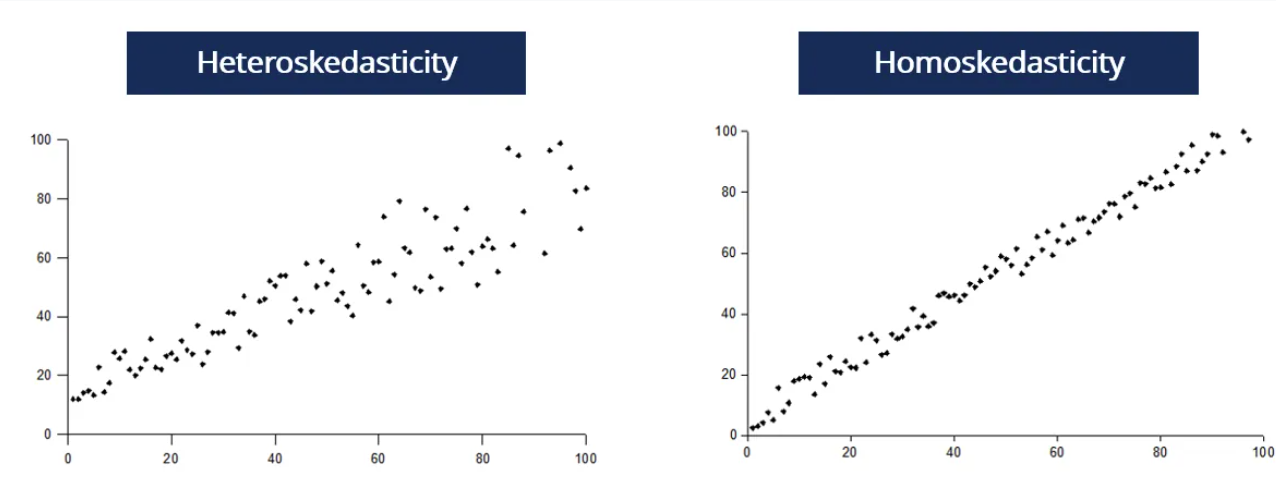출처 : CFI Education Inc. Heteroskedasticity
3) 비상관 : $E[\,X\epsilon\,] = 0 \quad \Rightarrow \quad \hat\beta_{OLS}$ 는 일관적 : 일치추정
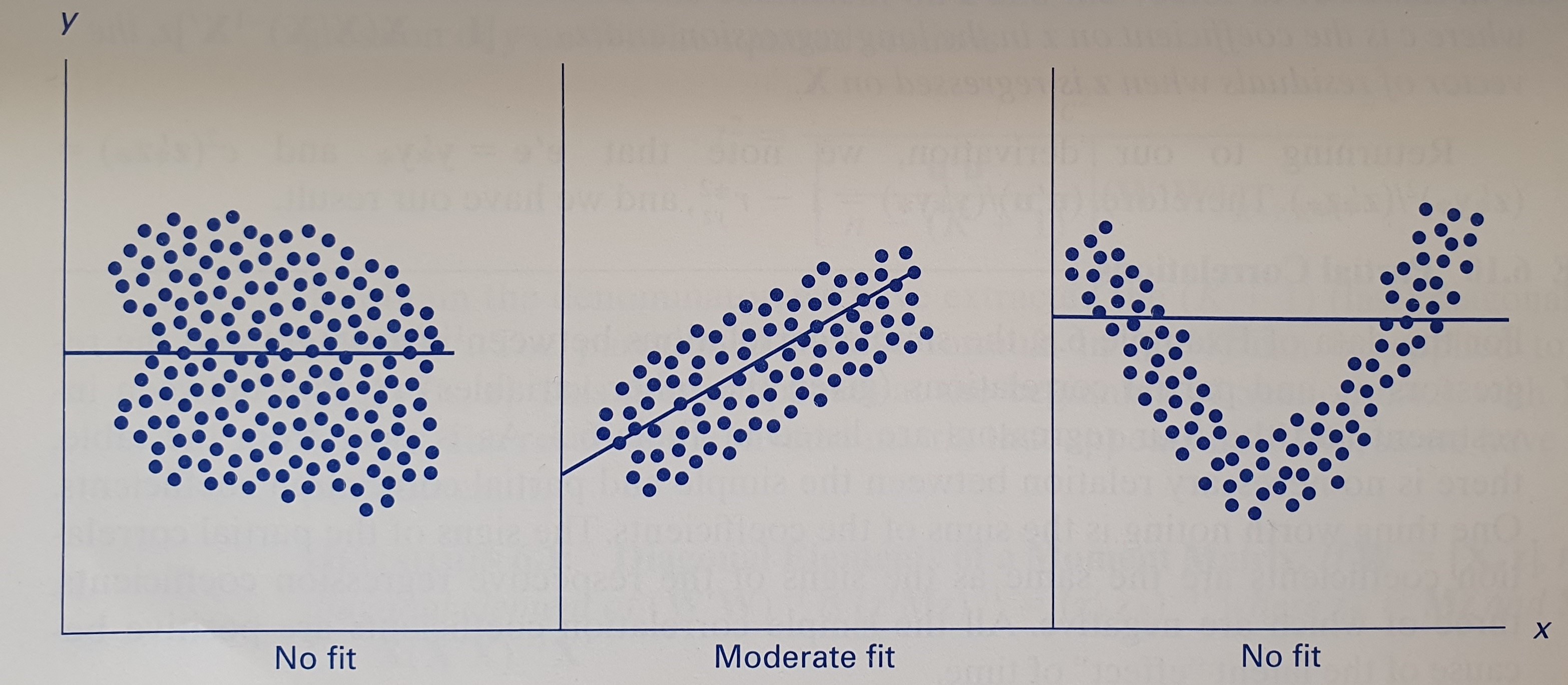출처 : W. H. Greene, Econometric Analysis
4) 상관 : 내생성 endogeneity : $E[\,X\epsilon\,] \ne 0$
-
패널/시계열 등 상관구조 추론 가능 $\Rightarrow$ 적절한 방법론
-
상관구조 추론 어렵다면 $\Rightarrow$ 도구변수 등 특별조치
-
도구변수: $X$ 와 상관인 동시에 $\epsilon$ 과는 비상관
